Cryptographie

La cryptographie est la science qui utilise les mathématiques
afin de crypter et décrypter des données.
Grâce à la cryptographie, on peut ainsi transmettre des
données sensibles (confidentielles) en utilisant des canaux de communication
qui ne sont pas sûr (par exemple Internet).
Seule la personne destinataire des données pourra les lire.
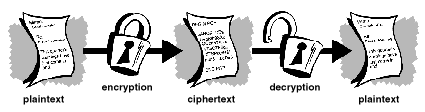
<Figure 1-1 sur le site http://www.pgpi.com/doc/pgpintro/>
Cryptographie à clé privée (cryptographie
conventionnelle)
C'est la méthode la plus simple (et la moins sûre !) pour
crypter/décrypter des données.
Elle utilise la même clé afin de chiffrer et déchiffrer
le message. Cette méthode est dite à clé symétrique,
ou à substitution.
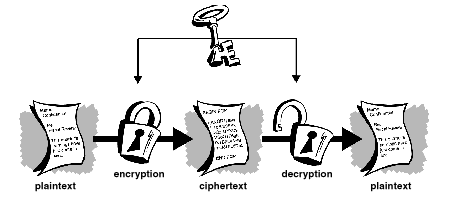
<figure 1-2 sur le site http://www.pgpi.com/doc/pgpintro/>
Ex. : Jules César envoyait des messages codés à
ses généraux en utilisant un codage à décalage
par 3 (A=>D, B=>E, C=>F, ..., F=>I, ..., I=>L, ..., W=>Z, ...)
Message en clair : SECRET
Message codé : VHFUHW

La clé (ici, décalage par 3), doit être connue de
l'expéditeur et du destinataire.
=> Problème, comment communiquer une clé par un canal
de communication qui n'est pas sûr ?
On sait statistiquement la proportion d'apparition d'une lettre de l'alphabet
dans un texte écrit dans une langue donnée.
Ainsi, le cryptage étant simplement le remplacement d'une lettre
par une autre, il est facile d'établir une statistique des lettres
du texte codé, et de comparer à la statistique originale,
comme ci-dessous, dans le cas de l'anglais :

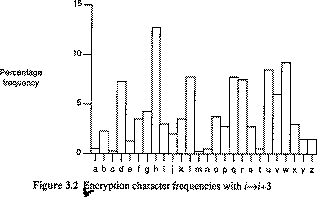
Cryptographie à clé publique
1975 - Concept introduit par Diffie et Hellman (mais existait probablement
depuis 1970 en Grande-Bretagne (secret militaire)).
Dans ce type de codage, dit asymétrique, deux clés différentes
rentrent en jeu.
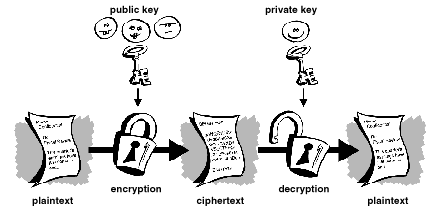
<Figure 1-3 sur le site http://www.pgpi.com/doc/pgpintro/>
Clé publique : utilisée par l'expéditeur afin de
crypter les données.
Clé privée : utilisée uniquement (et gardée
secrète) par le destinataire afin de décrypter le message.
Il est impossible mathématiquement de déduire (calculer)
la clé privée si l'on connait la clé publique.
Avec cette technique de cryptage, il n'y a plus de problème pour
communiquer.
La clé publique peut être transmise directement à
la personne qui souhaite envoyer un message crypté.
Signature
La signature permet de certifier la provenance de données.
Avant de crypter les données avec la clé publique du destinataire,
l'émetteur ajoute une signature aux données en fonction des
données et de sa clé privée.
Il peut ensuite crypter l'ensemble avec la clé publique du destinataire,
puis lui envoyer.
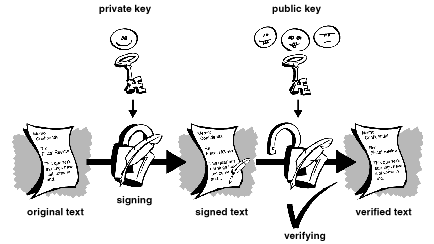
<Figure 1-6 sur le site http://www.pgpi.com/doc/pgpintro/>
Intégrité des données
Cette fonctionnalité permet de s'assurer que les données
n'ont pas été altérées.
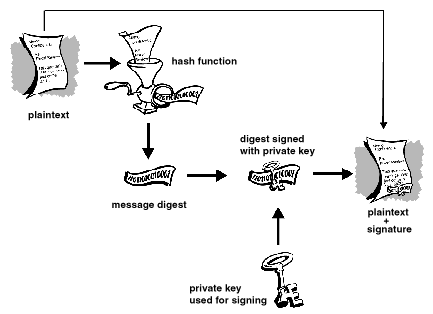
<Figure 1-7 sur le site http://www.pgpi.com/doc/pgpintro/>
Algorithmes
Généralement en utilisant des calculs
à partir de nombres premiers très grands.
-
DES (Data Encryption Standard)
Connu aussi sous le nom DEA (ANSI) et DEA-1 (ISO)
Standard depuis 1975 environ suite à une réflexion entre
le gouvernement américain (NSA) et des sociétés privées
Pour pouvoir revendiquer l'utilisation de l'algorithme DES, le produit
doit être validé par NIST
Algorithme performant (utilisé pour les transactions bancaires
sur Internet)
Code-source largement diffusé
Utilisable dans différents domaines (informatique, électronique,
radio, ...)
Code pouvant être "cassé" par la NSA en 3 à 11 minutes
en utilisant un CRAY Y-MP (c'est une rumeur !)
Plusieurs variantes : Triple-DES, ...
-
Diffie-Hellmann : Whitfield DIFFIE, Martin HELLMANN (1976)
Algorithme utilisé principalement pour la gestion des clés
-
RSA : Ron RIVEST, Adi SHAMIR, Leonard ADLEMAN
Algorithme le plus facile à comprendre => Standard de l'industrie
(40 à 2048 bits)
Les clés sont calculées à partir de deux nombres
premiers très grands
Aucune preuve qui démontre les bases de RSA (ni qui prouve que
la théorie est fausse)
Algorithme dont l'utilisation est payante avant le 20/09/2000 et gratuite
ensuite.
-
RC2
Algorithme à clé de taille variable développé
par RSA
Implémentation très méconnue
-
IDEA
L'un des meilleurs algorithmes de cryptographie symétrique
Intégré à PGP
Libre de droits pour un usage privé
-
CAST
Algorithme à base de clés 128 bits
Pas de méthode permettant de casser le code, à part l'attaque
massive
Voir la RFC 2144 pour tous les détails
-
Elgamal : par Taher ELGAMAL
Basé sur le calcul logarithmique discret
Algorithme dans le domaine public depuis le 29/04/1997
-
ECC (Eliptic Curve Cryptosystem)
N. KOBLITZ et V.S. MILLER (1985)
Utilise des algorithmes standards => vitesse de cryptage + clé
de relativement petite taille
-
DSA : Digital Signature Algorithm (David KRAVITZ)
-
Blowfish
Algorithme très compact, dans le domaine public
Quelques faiblesses
Clés
Cryptographie à clé privée
La performance dépend de :
-
l'algorithme utilisé
-
la longueur de la clé
|
Coût du matériel utilisé
|
40 bits
|
56 bits
|
64 bits
|
80 bits
|
112 bits
|
128 bits
|
| 100 K$ |
2 s |
35 h |
365 j |
70 000 ans |
10e14 ans |
10e19 ans |
| 1 M$ |
0.2 s |
3.5 h |
37 j |
7 000 ans |
10e13 ans |
10e18 ans |
| 10 M$ |
0.02 s |
21 min |
4 j |
700 ans |
10e12 ans |
10e17 ans |
| 100 Md$ |
2e-6 s |
0.1 s |
32 s |
24 j |
10e8 ans |
10e13 ans |
(Source : Applied Cryptography 2nd edition : 1995) pour une attaque
massive
Si on utilise un cluster de machines (400 machines) pouvant traiter
32000 codes par seconde (chacune), il faudrait à peine 1 jour pour
une clé de 40 bits
Une clé de 128 bits est par contre (à l'heure actuelle)
jugée inviolable.
Cryptographie à clé publique
1977 : R. RIVEST annonce qu'il faudrait environ 40e15 années pour
factoriser un nombre de 125 digits.
1994 : Un nombre de 129 digits a réussi à être
factorisé.
Recommandation de taille de clés publique (Source : Applied Cryptography
2nd edition)
| Année |
Utilisation privée |
Utilisation commerciale |
Utilisation gouvernementale |
| 1995 |
768 bits |
1280 bits |
1536 bits |
| 2000 |
1024 bits |
1280 bits |
1536 bits |
| 2005 |
1280 bits |
1536 bits |
2048 bits |
| 2010 |
1280 bits |
1536 bits |
2048 bits |
| 2015 |
1536 bits |
2048 bits |
2048 bits |
Comparaison de taille de clés
Pour un cryptage avec une sécurité sensiblement similaire
face une attaque massive
| Cryptographie symétrique (clé publique) |
Cryptographie asymétrique (clé privée/clé
publique) |
| 56 bits |
384 bits |
| 64 bits |
512 bits |
| 80 bits |
768 bits |
| 112 bits |
1792 bits |
| 128 bits |
2304 bits |
(Source : Applied Cryptography 2nd edition)
Rappel : il n'y a pas que la longueur de la clé qui rentre
en compte dans la sécurité; La complexité de l'algorithme
utilisé est également à prendre en compte.
Génération de clés
Généralement les clés sont générées
à partir de données aléatoires (mouvement de la souris,
touches clavier, heure, informations spécifique au poste informatique).
Dans le cas de la clé privée, la clé est stockée
sous forme codée sur l'oridnateur en utilisant une "phrase de passe".
Contre la cryptographie
-
Attaques brutales :
-
distributed.net : propose de (participer
à) casser les algorithmes RC5-64 (en cours), DES-II (terminé)
et RC5-56 (terminé)
Projet de calcul distribué à l'initiative d'un programmeur
indépendant du Colorado Rocke Verser suite à la proposition
de la société RSA qui offre
10 000 $ (en Janvier 1997) au premier programmeur qui cassera une clé
de 56 bits (72 057 594 037 927 936 combinaisons) => 2285 ans pour un seul
ordinateur personnel
20% des combinaisons testées en 3 jours à peine (lors
de la 3ième tentative en juillet 1998)
-
RSA Labs : propose un challenge visant à casser le code RSA (40
à 2048 bits)
-
1999 : 12 minutes pour un code de 40 bits avec 60000 F de matériel
(moins d'une journée pour un étudiant)
-
1999 : 13 heures pour un code de 56 bits avec 60 MF de matériel
-
08/1999 : association de 6 laboratoires pour casser un code de 512 bits
-
Entrées cachées (backdoors)
Réexpédier un message codé à un destinataire
secret (le gouvernement !!)
=> Vérifier en contrôlant le code source (preuve de confiance)
-
Exploitations de la faiblesse des algorithmes
Certains algorithmes ont des performances différentes suivant
l'ordre des opérations (signature puis encryptage ou l'inverse)
-
Méthodes non-informatiques
-
Capture clavier
-
Relevé visuel du mot de passe (phrase de passe)
-
Espionnage électromagnétique des informations claviers et
souris
-
Usurpation d'identité (administrateur réseau, directeur,
...)
-
Détection des textes cryptés
-
On détecte l'en-tête du fichier (Word, Excel, Postscript,
...)
-
On essaie de décompresser le fichier avec différents algorithmes
de compression (ZIP, ARJ, RAR, GZ, ...)
-
Si, après tous ces essais, on n'obtient rien de "lisible", alors
le fichier est probablement crypté








